Intro
What are transducers? The basic idea is to extract the essence of map, filter and other functions that transform sequences and collections, and reuse this essence so that it can be applied elsewhere; to recast them as process transformations.
The kind of process for which we can use transducers is a succession of steps, where each step is ingesting an input. Building a collection is just one example of a process of that shape. But let us not focus on the idea of a process which performs building. Some processes build particular things, other processes are infinite.
Why it’s called transducer? It’s a real world and it’s better than reduce or ingest, which could be considered.
- reduce: lead back, brings something back
- ingest: carry into
- transduce: lead across; as inputs are carried into the process, they are led through a series of transformations
Transducers are not a programming thing. We have them in real life, where we usually call them “instructions”. For example, consider the instruction to baggage carriers “put the baggage on the plane”. While you’re doing it:
- break apart pallets
- remove bags that smell like food
- label heavy bags
There could be different circumstances (conveyances, sources, sinks). They are irrelevant. Does baggage come and go on trolleys or conveyor belts? We don’t care and we don’t want to care. This is the real world: unspecified and flexible.
In programming we have something like this — collection function composition:
(comp
(partial mapcat unbundle-pallet)
(partial filter non-food?)
(partial map label-heavy))
There’s a big difference between real world and this programming approach. map, filter, mapcat are functions of sequence → sequence. We model the rules, but they only work on sequences. When we get something new, like stream, channel or observable, none of the rules apply.
Another problem is that this code creates intermediate sequences between steps. It’s as if we told the baggage guys to take the baggage off the trolley, unbundle, put bags on another trolley, check for food smell, put bags on another trolley, etc.
There is no reuse. Every new collection or a process defines its own version of map, filter, mapcat etc. As a result, composed algorithms are needlessly specific and inefficient.
Creating and using transducers
Let’s start with the value propositions right away. This is what we want to achieve. First, we create a transducer process-bags, which is a composition of three transducers.
(def process-bags
(comp
(mapcatting unbundle-pallet)
(filtering non-food?)
(mapping label-heavy)))
mapcatting, filtering and mapping return transducers. process-bags is a transducer. Transducers modify a process by transforming its reducing function. Once done, we can go to a completely different context and reuse them.
Building a concrete collection. Standard function into now has another arity: it can accept a transducer to generate a collection out of something else.
(into airplane process-bags pallets)
sequence can now take a transducer as well and generate a lazy sequence of values.
(sequence process-bags pallets)
A new function transduce works like reduce, but takes a transducer, operation, initial value and the source. Here we count the total weight of the bags:
(transduce
;; transducer
;; ↓
(comp process-bags (mapping weigh-bag))
;; operation
;; ↓
+ 0 pallets)
;; ↑ ↑
;; | source
;; initial value
This also should work for channels, observables and other contexts:
;; a CSP channel that processes bags
(chan 1 process-bags)
;; it's an open system
(observable process-bags pallet-source)
We call processes that can work with transducers (like into, sequence, chan, etc) transducible processes. They accept a transducer and use it to transform whatever they do. So, the notion of a transducer has two parts:
- Functions that create transducers.
- In context where they make sense, you accept transducers.
Each process takes a transducer and their internal processing function. What’s the internal processing function of into? It’s conj (in Clojure). Channels are inherently the same, they take input and somewhere inside they have a step function: add the item to the buffer. That step function has the same shape as conj. So, into and channel can transform their internal operations with the help of transducers.
Two papers which describe this idea are:
- Lectures on Constructive Functional Programming, by Richard S. Bird
- A tutorial on the universality and expressiveness of fold, Graham Hutton
How do we get there?
Let’s now discuss how can we achieve this. We’ll start by re-defining map, filter and mapcat.
One of the things discussed in the first mentioned paper is the relationship between list processing operations and fold. There’s some interesting math that proves the equivalency of lists and operations that construct them. Map and filer can be defined via foldr, which encapsulates recursion and makes it easier to reason about and transform data:
(defn mapr [f coll]
(foldr (fn [x r] (cons (f x) r))
() coll))
(defn filterr [pred coll]
(foldr (fn [x r] (if (pred x) (cons x r) r))
() coll))
You can similarly re-define these functions in terms of foldl, which is just left reduce. Right reduce implies laziness, right reduce implies loops. It turns up that the loop path is faster, better and more general for the goals we try to achieve.
(defn mapl [f coll]
(reduce (fn [r x] (conj r (f x)))
[] coll))
(defn filterl [pred coll]
(reduce (fn [r x] (if (pred x) (conj r x) r))
[] coll))
(defn mapcatl [f coll]
(reduce (fn [r x] (reduce conj r (f x)))
[] coll))
In both left and right cases, it’s mostly boilerplate, and the fundamental thing all functions do is the same: here’s the thing that to do to all the things that come through. The problem here is conj. It is a specific operation in the middle of those generic ideas of map, filter and mapcat. conj might not be what we want to do.
To turn those inner functions into transducers we need to add another layer, and allow passing arbitrary step operation instead of hard-coding conj.
(defn mapping [f]
(fn [step]
(fn [r x] (step r (f x)))))
(defn filtering [pred]
(fn [step]
(fn [r x] (if (pred x) (step r x) r))))
(def cat
(fn [step]
(fn [r x] (reduce step r x))))
(defn mapcatting [f]
(comp (map f) cat ))
Now mapping takes a function and returns a function which expects a step function as argument. We can now pass conj and produce the reduce-based map, filter and mapcat:
(defn mapl [f coll]
(reduce ((mapping f) conj)
[] col))
(defn filterl [pred coll]
(reduce ((filtering pred) conj)
[] coll))
(defn mapcatl [f coll]
(reduce ((mapcatting f) conj)
[] coll))
That was the whole point. Transducers are fully decoupled. They know nothing about the process they modify.
Transducers are fast
One benefit of transducers is speed. Since they are just a stack of function calls, there’s no laziness overhead, no intermediate collections, no extra “boxes”. There’s no notion of “empty list is nothing”. Nothing is nothing, an empty list is an empty list.
Transducer types
Transducers raise interesting problems in the context of type theory.
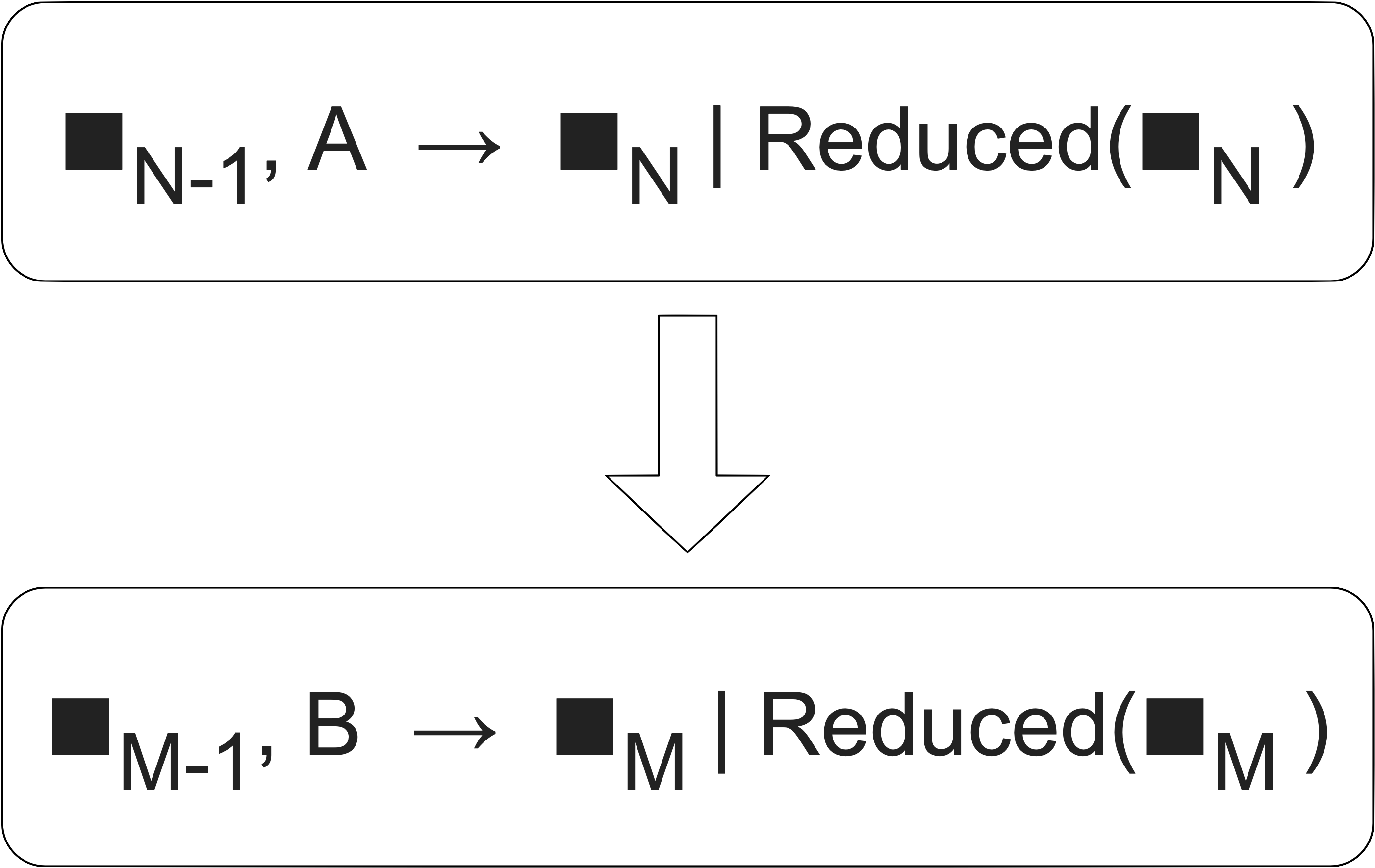
If you’re trying to produce the next process N, you must supply the result of step N-1 as input. Thus, modeling the type system as R→R would be wrong. We’d need something like this:

Also, the black boxes that represent the elements are unnecessarily restrictive by type in this image. We could create a step function that when input is x the output is y, when input is y the output is z, when input is z the output is x. It’s a perfectly fine state machine, but it’d be tricky to figure out the type system for that. {x,y,z}→{x,y,z} is not the answer, because for input x the output must be only y, not x or y or z.
Early termination
Ordinary reduction processes everything. Sometimes a process has a reason to terminate early, for whatever reason. It maybe the desire of the process itself, or a decision of one of the steps, or an external trigger.
Continuing with the baggage handling analogy, let’s say if the bag is ticking — that’s it, go home.
(comp
(mapcatting unbundle-pallet)
(taking-while non-ticking?)
(filtering non-food?)
(mapping label-heavy))
taking-while must stop the whole job. How to do that? Turns out in Clojure reduce can already do that via (reduced result). It’s a wrapper with a corresponding test reduced?. Once wrapped, we can dereference the value with deref:
(reduced? (reduced x)) ;; → true
(deref (reduced x)) ;; → x
Transducers support reduced. That means that step functions can return (reduced value). If a transducer gets a reduced value from a nested step call, it must never call that step function again with input.
(defn taking-while [pred]
(fn [step]
(fn [r x]
(if (pred x)
(step r x)
(reduced r)))))
All reducing processes must also support reduced. If the step function returns a reduced value, the process must not supply any more input to the step function. The dereferenced value is the final accumulated value.
To illustrate this improvement in the context of types, we’d need to build something like this:
Vertical bar represents OR. I.e. a process returns a black box or a reduced version of it.
State
Some interesting sequence functions require state (e.g. take, partition-*). They might count stuff or accumulate a sum, for example. Where would that data go? In purely functional approach the stack or laziness can be used to capture state. The idea of transducers is to isolate the execution completely, so we can’t use that approach.
State has to be explicit. It must be incorporated into the transducer object. They must create unique state every time they are called upon to transform a step function. Thus, once applied to a process, a transducer yields another (potentially stateful) process.
You should always treat an applied transducer stack as if it returned a stateful process, because you don’t know until the end whether there’ll be state. This means you can’t alias the process returned by a transducer.
Here’s an example of a stateful transducer:
(defn dropping-while [pred]
(fn [step]
(let [dv (volatile! true)]
(fn [r x]
(let [drop? @dv]
(if (and drop? (pred x))
r
(do
(vreset! dv false)
(step r x))))))))
That’s not the prettiest thing…
Completion
Some jobs don’t complete, they don’t have ends, they don’t consume finite collections. They might accept things from a channel or a event source.
But other jobs might complete (stop receiving input). A process might want to do a final transformation of the value built up. A stateful transducer might want to flush a pending value. So, all step functions must have an arity-1 variant that does not take an input.
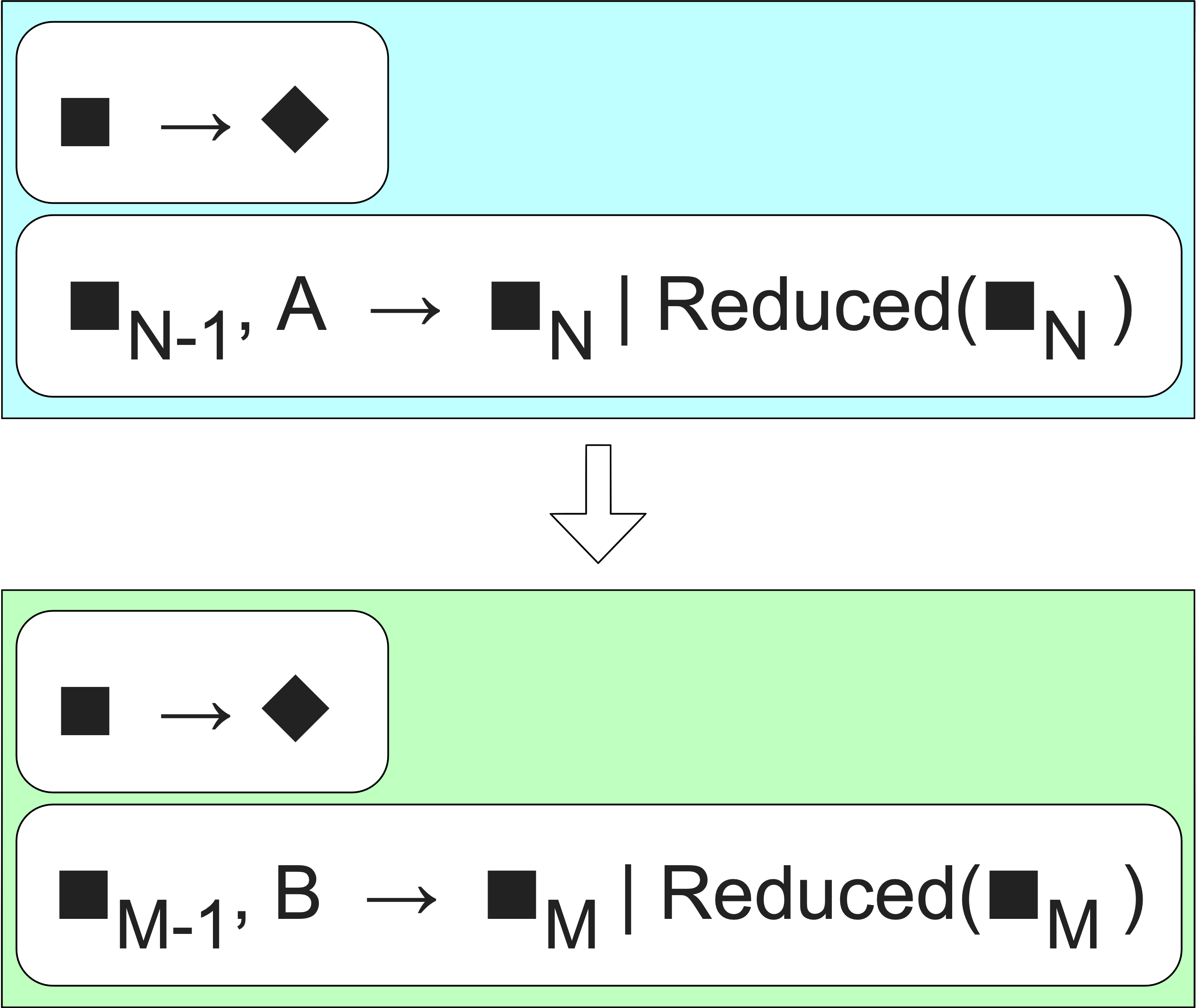
If the process has finished, it must call the completion operation exactly once. Each transducer must do the same thing and call its nested completion operation. It may flush state using the nested step function prior to calling nested complete.
Coming back to the visual types, we now have to think of reducing function as a pair of operations. The first takes no input — that’s the completion operation. The second is the regular step operation.
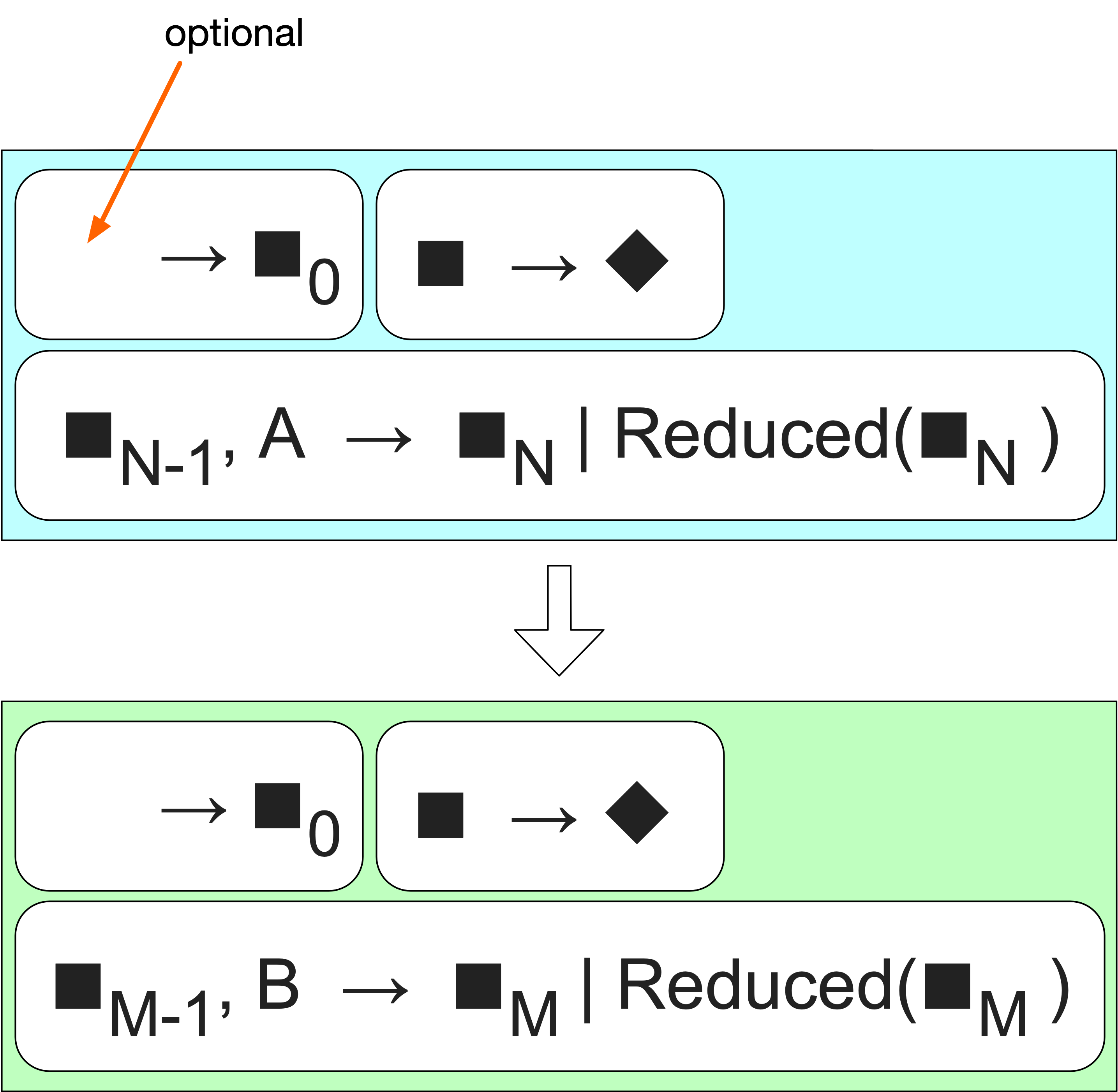
Init
There’s the third type of operation that’s associated with processing in general: init. A reducing function may support arity-0 which returns an initial accumulation value. Transducers must support arity-0 in terms of a call to the nested init.
(+) ;; → 0
(+ 21) ;; → 21
(*) ;; → 1
We now have three operations, one of which is init from nothing.
In Clojure we just define functions with arity 0, 1, 2. Transducers take and return reducing functions. Now, core sequence functions’ 1-arity variant return a transducer. We decided not to call those things mapping, filtering, etc (as this may not carry very well into languages other than English). So, to create a transducer, call a function without the collection:
(mapping f) == (map f)
This applies to core sequence functions:
mapmapcatfilterremovetaketake-whiledropdrop-whiletake-nthreplacepartition-bypartition-allkeepkeep-indexedcatdedupe- etc…
Here’s the final example: filter returning a transducer. It takes a predicate and returns a step modifying function, which takes a reducing function which presumably has # arities, and defines a function with three arities:
- init
- complete, which in case of filter just returns the result
- the result of input, which is what regular filter does
(defn filter
([pred]
(fn [rf]
(fn
([] (rf))
([result] (rf result))
([result input]
(if (pred input)
(rf result input)
result)))))
([pred coll]
(sequence (filter pred) coll)))
Summary
Transducers:
- support early termination and completion
- are context-independent
- reusable across a wide variety of contexts
- composable via ordinary function composition
- efficient
This is a complete summary of an excellent talk by Rich Hickey “Transducers”. Illustrations and diagrams are recreated; source code taken verbatim from the slides, except for comments, which were extended in some places.
(You can get a set of PDF/HTML/epub/Kindle versions below. Name your price, starting from $1.)